ᐈ корреляция и причинно-следственная связь

Измерение корреляции

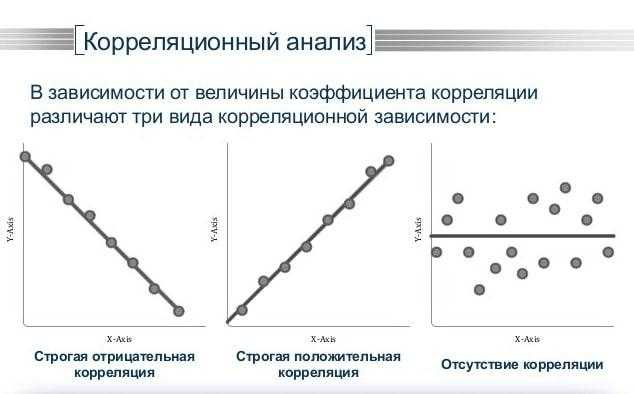
Статистика предлагает измерять корреляционную взаимосвязь с помощью числового коэффициента, в который будет входить ее величина и направление. Чем больше это число, тем сильнее взаимная связь параметров. Направление взаимодействия будет определяться знаком коэффициента корреляции.

Отрицательный знак будет означать, что уменьшение одной величины ведет к росту другой. Например, уменьшение количества бензина, выдаваемого полицейским патрульным машинам, приведет к повышенным показателям хулиганских действий на улицах.

При отсутствии корреляции говорят, что она равна нулю. Уровень воды в реке во время паводка может быть никак не связан с количеством заболеваний гриппом.

Как сформировать сбалансированный облигационный портфель

Критерии формирования портфеля облигаций зависят от многих факторов, в том числе от целей и сроков вложения, требования к сохранности вложений и уровня толерантности инвестора к риску.

Стоит также учитывать зависимость облигации от ключевой ставки ЦБ — ее изменение влияет на цену облигации, замечает инвестиционный консультант «ВТБ Мои Инвестиции» Никита Мурлейкин. Чем больше срок погашения, тем сильнее будет меняться цена облигации при изменении процентных ставок.

«Например, если рынок закладывает повышение ставки ЦБ, то стоимость облигаций может снизиться. И чем дальше срок погашения облигации, тем сильнее может снизиться ее цена», — отмечает он.

Поэтому при формировании портфеля из облигаций стоит придерживаться правила: чем выше риск эмитента, тем ниже доля его облигаций в портфеле и меньше дюрация, считает главный аналитик Банки.ру Богдан Зварич.

По его мнению, основу портфеля лучше формировать, делая упор на надежные инструменты, такие как ОФЗ и облигации крупных корпоративных эмитентов. При этом для диверсификации по валютам можно рассматривать не только рублевые инструменты, но и, например, облигации в юанях, и замещающие облигации, добавляет эксперт.

Послесловие

В рамках данного обзора, вы узнали что такое корреляция, какие виды бывают, что представляет собой коэффициент корреляции и для чего он может применяться.

Отмечу, что всегда стоит помнить про здравую логику и что у вас своя голова. Корреляция — это вероятностная характеристика, полученная оценкой уже произошедших событий. Поэтому она может быть полезной, но не стоит ее считать полноценным фактором, гарантирующим те или иные варианты развития событий.

К примеру, если год за годом ваши доходы были практически равны расходам, то это совершенно не означает, что в этом году вы не задумаетесь о финансовой подушке безопасности и поэтому ваши расходы резко уменьшатся.

Как выбирать между государственными, региональными и корпоративными облигациями

Традиционно самыми надежными среди облигаций считаются ОФЗ, так как заемщиком выступает государство. При этом и доходность таких бумаг самая низкая. Затем идут региональные, муниципальные и корпоративные бумаги: доходность выше, чем у ОФЗ, но также выше и риск дефолта.

«При покупке муниципальных облигаций стоит учитывать, что ни Минфин, ни правительство России, ни Центральный банк не несут ответственности по долговым обязательствам субъектов и муниципальных образований. Облигации крупных субъектов — Москвы, Санкт-Петербурга, Московской области — торгуются на уровне чуть выше, чем доходности госбумаг», — говорит Мурлейкин.

В целом распределение вложений в облигации зависит от ожидаемой доходности и сроков инвестиций, а также от отношения клиента к риску вложений в корпоративный долг.

Чем терпимость инвестора к риску ниже, тем большую долю портфеля нужно аллоцировать на более надежные инструменты, то есть ОФЗ и крупные эмитенты корпоративных облигаций, говорит Зварич. По его мнению, доля одного корпоративного эмитента не должна превышать 10% от портфеля.

«Оставшуюся часть можно распределить между менее надежными корпоративными облигациями и сектором высокодоходных облигаций. Здесь долю средств от портфеля, направляемую в бумаги одного эмитента, лучше сократить до 3–5%», — считает он.

Для долгосрочных вложений на срок 10–18 лет в настоящий момент можно инвестировать с минимальным кредитным риском в государственные облигации (или так называемое ОФЗ-ПД с погашением в 2033–2041 годах), говорит аналитик долговых рынков БК «Регион» Александр Ермак. Эффективная доходность по ним составляет 10,6–10,8% годовых, замечает он.

Консервативным инвесторам, для которых наиболее важны сохранность вложений и минимальный риск их потерь, целесообразнее всего инвестировать в корпоративные облигации первого эшелона (с наиболее высоким кредитным качеством) на срок 2–3 года, считает Ермак. Эффективная доходность по ним в настоящее время составляет порядка 9,10–10,10% годовых, уточняет он.

«С такой доходностью торгуются на Московской бирже облигации широкого круга эмитентов, например «Газпром Капитал», «Роснефть», «Норникель», РЖД, «Русгидро», «Почта России», МТС, «Магнит», Сбербанк, Россельхозбанк», — перечисляет эксперт.

Порядка 10,5–11,5% годовых составляет эффективная доходность облигаций второго эшелона, среди которых ценные бумаги таких эмитентов, как ГК «Автодор», ГТЛК, АФК «Система», добавляет он.

Примеры

Необходимо определить взаимосвязь двух переменных: уровня интеллектуального развития (по данным проведенного тестирования) и количества опозданий за месяц (по данным записей в учебном журнале) у школьников.

Исходные данные представлены в таблице:

№	Данные по уровню IQ (x)	Данные по количеству опозданий (y)
1	100	6
2	115	2
3	117	1
4	119	1
5	134	2
6	94	8
7	105	3
8	103	4
9	111	3
10	124
Сумма	1122	30
Среднее арифметическое	112,2	3

Чтобы дать правильную интерпретацию полученному показателю, необходимо проанализировать знак коэффициента корреляции (+ или -) и его абсолютное значение (по модулю).

В соответствии с таблицей классификации коэффициента корреляции по силе делаем вывод о том, rxy = -0,827 – это сильная отрицательная корреляционная зависимость. Таким образом, количество опозданий школьников имеет очень сильную зависимость от их уровня интеллектуального развития. Можно сказать, что ученики с высоким уровнем IQ опаздывают реже на занятия, чем ученики с низким IQ.

Важно! Принято считать, что чем r ближе по модулю к 1, тем ближе связь между анализируемыми переменными к линейной. Если величина r близка к -1, то связь обратная (c возрастанием переменной х переменная у убывает).. Коэффициент корреляции может применяться как учеными для подтверждения или опровержения предположения о зависимости двух величин или явлений и измерения ее силы, значимости, так и студентами для проведения эмпирических и статистических исследований по различным предметам

Необходимо помнить, что этот показатель не является идеальным инструментом, он рассчитывается лишь для измерения силы линейной зависимости и будет всегда вероятностной величиной, которая имеет определенную погрешность

Коэффициент корреляции может применяться как учеными для подтверждения или опровержения предположения о зависимости двух величин или явлений и измерения ее силы, значимости, так и студентами для проведения эмпирических и статистических исследований по различным предметам. Необходимо помнить, что этот показатель не является идеальным инструментом, он рассчитывается лишь для измерения силы линейной зависимости и будет всегда вероятностной величиной, которая имеет определенную погрешность.

Корреляционный анализ применяется в следующих областях:

экономическая наука;
астрофизика;
социальные науки (социология, психология, педагогика);
агрохимия;
металловедение;
промышленность (для контроля качества);
гидробиология;
биометрия и т.д.

Причины популярности метода корреляционного анализа:

Относительная простота расчета коэффициентов корреляции, для этого не нужно специальное математическое образование.
Позволяет рассчитать взаимосвязи между массовыми случайными величинами, которые являются предметом анализа статистической науки. В связи с этим этот метод получил широкое распространение в области статистических исследований.

Коэффициент корреляции[]

Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.

Коэффициент корреляции Пирсона

Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:

Пусть X,Y{\displaystyle X, Y} — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

ϱX,Y=cov(X,Y)DX⋅DY{\displaystyle \varrho_{X,Y} = \frac{\mathrm{cov}(X,Y)}{\sqrt{\mathrm{D}} \cdot \sqrt{\mathrm{D}}}},

где cov{\displaystyle \mathrm{cov}} обозначает ковариацию, а D{\displaystyle \mathrm{D}} — дисперсию, или, что то же самое,

ϱX,Y=EXY−EX⋅EY(EX2−(EX)2)⋅(EY2−(EY)2){\displaystyle \varrho_{X,Y} = \frac{\mathbb{E}-\mathbb{E}X \cdot \mathbb{E}Y} {\sqrt{(\mathbb{E}-(\mathbb{E}X)^2)} \cdot \sqrt{ (\mathbb{E}-(\mathbb{E}Y)^2)}}},

где символ E{\displaystyle \mathbb{E}} обозначает математическое ожидание.

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и с номинальной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ{\displaystyle \tau} (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).

Свойства коэффициента корреляции

Неравенство Коши — Буняковского:

если принять в качестве скалярного произведения двух случайных величин ковариацию ⟨X,Y⟩=cov(X,Y){\displaystyle \langle X, Y \rangle = \mathrm{cov}(X, Y)}, то норма случайной величины будет равна ‖X‖=DX{\displaystyle \|X\| = \sqrt{\mathrm{D}}}, и следствием неравенства Коши — Буняковского будет:

−1⩽ϱX,Y⩽1{\displaystyle -1 \leqslant \varrho_{X,Y} \leqslant 1}.

Коэффициент корреляции равен ±1{\displaystyle \pm 1} тогда и только тогда, когда X{\displaystyle X} и Y{\displaystyle Y} линейно зависимы:

ϱX,Y=±1⇔Y=kX+b,k≠{\displaystyle \varrho_{X,Y} = \pm 1 \Leftrightarrow Y = kX+b, k\neq0},

где k,b∈R{\displaystyle k,b\in \mathbb{R}}. Более того в этом случае знаки ϱX,Y{\displaystyle \varrho_{X,Y}} и k{\displaystyle k} совпадают:

sgn⁡ϱX,Y=sgn⁡k{\displaystyle \operatorname{sgn} \varrho_{X,Y} = \operatorname{sgn} k}.

Если X,Y{\displaystyle X, Y} независимые случайные величины, то ϱX,Y=0{\displaystyle \varrho_{X,Y} = 0}. Обратное в общем случае неверно.

Типы инвестиционных портфелей по степени риска

Состав оптимального портфеля определяется целью, которую хочет достигнуть инвестор. Это может быть:

•

постоянный стабильный доход;
•

быстрый возврат капитала;
•

динамичное или умеренное наращивание вложений.

Чем более рискованные инструменты используются для формирования портфеля инвестиций, тем выше уровень потенциальной прибыли. Профессиональные инвесторы всегда имеют несколько наборов активов с разными характеристиками.

Консервативный портфель инвестиций

Консервативный портфель — это умеренно рисковый и, как следствие, менее прибыльный портфель, состоящий из краткосрочных займов, облигаций и других инструментов с минимальной степенью риска.

Основная цель инвестиционных инструментов такого типа — это сохранение капитала и получение хотя бы минимального, но регулярного дохода.

В основе портфельного инвестирования с низким риском и стабильной прибылью могут использоваться следующие инструменты:

•

Облигации федерального займа (ОФЗ). Желательно выбирать бумаги с рейтингом А и выше.
•

Акции категории «голубые фишки». Это ценные бумаги крупнейших компаний с высокой капитализацией. Они имеют низкую волатильность — цена стабильно растёт, без резких скачков.
•

Драгоценные металлы: золото, платина и другие.
•

Депозиты в банках с рейтингом А и более.
•

Недвижимость в странах со стабильной экономикой — Великобритании, Франции, Германии, США и в других.

Средняя доходность консервативного инвестиционного портфеля составляет 4–12% в год.

При выборе отдельных активов нужно учитывать возможное изменение их стоимости в ближайшие 5 лет, а также обращать внимание на показатели инфляции

Умеренный портфель

Умеренный портфель. Умеренность заключается в использовании инструментов с низким и средним уровнем рисков. Первые обеспечивают стабильный доход, вторые — более высокую прибыль. В сумме такие активы дают средний уровень рисков и прибыли.

Принципы формирования умеренного инвестиционного портфеля предполагают использование следующих инструментов:

•

Государственные и корпоративные облигации. Рекомендуется покупать 7–8 разных активов этой группы.
•

ETF-фонды. Инвестор платит брокерскую комиссию за одну акцию, при этом сам фонд может работать с десятками и сотнями прибыльных активов. Это один из самых простых и доступных способов получить прибыль от дорогих акций.
•

Паевые инвестиционные фонды. Пай даёт доступ к владению частью целого набора инструментов. Поскольку доход формируется за счёт работы с разными активами, риск потери средств остаётся низким.

Биржевые фонды хороши тем, что в них за управление деньгами инвесторов отвечают профессионалы. Сами фонды могут отличаться по типу своей работы:

•

индексные;
•

товарные;
•

индустриальные;
•

инверсионные;
•

облигационные и прочие.

Также крупные компании могут формировать собственные ПИФы и ETF. То есть выбор действительно большой: можно выбрать надёжные инструменты с разным уровнем доходности.

Умеренный портфель обеспечивает прибыль в пределах 12–25% в год. Доля инструментов с высоким уровнем риска должна составлять не более 25%.

Агрессивный портфель инвестора

Основная задача такого набора активов — получить предельно высокую прибыль. Формируется агрессивный портфель из высокодоходных и рискованных инструментов. Риск не является целью, он просто неизбежен при таких вложениях.

Инструменты, подходящие для агрессивного стиля инвестирования:

•

акции быстро развивающихся стартапов;
•

высокодоходные облигации;
•

хедж-фонды;
•

опционы;
•

IPO — первичное размещение акций на фондовом рынке;
•

вложения в развитие стартапов;
•

фонды акций с высокими дивидендами;
•

недвижимость в странах, где возможен резкий скачок цен.

Доходность агрессивного инвестиционного портфеля составляет от 30% и выше. Границы риска и прибыли могут быть разными — всё зависит от предпочтений покупателя активов. Некоторые инвесторы сильно рискуют и получают 200–300% прибыли в год. Но такие вложения стоит делать только за счёт средств, которые можно безболезненно потерять в случае неверного прогноза.

Сбалансированный портфель

Опытные инвесторы часто комбинируют разные типы портфелей, не сосредотачиваясь на одном формате. Такой подход обеспечивает предельную диверсификацию и уровень дохода от среднего и выше.

Пример распределения капитала по разным направлениям:

•

консервативный — 30%;
•

умеренный — 35%;
•

агрессивный — 35%.

Значение корреляции в теории портфеля

Корреляция — это мера связи между двумя переменными. В теории портфеля, корреляция используется для определения связи между различными активами, входящими в портфель. Высокая корреляция означает, что два актива движутся в одном направлении, а низкая корреляция указывает на то, что два актива движутся в разных направлениях.

Корреляция является важным показателем в оценке риска портфеля. Если два актива имеют высокую корреляцию, то риск портфеля увеличится, так как изменение стоимости одного актива повлияет на изменение стоимости другого актива. Оптимальный портфель должен иметь активы с низкой или отрицательной корреляцией между ними.

Всякий раз, когда инвестор строит портфель, он должен учитывать корреляцию между различными активами. Это позволяет распределить риски между разными классами активов и максимизировать доходность при заданном уровне риска. Корреляционный анализ также дает инвестору возможность выявить и устранить дубликаты в портфеле, что позволяет диверсифицировать инвестиции.

Если инвестор не учитывает корреляцию при строительстве портфеля, то он рискует потерять все свои инвестиции в результате волатильности рынка. Корреляция позволяет инвестору диверсифицировать свой портфель и снизить риски, что в свою очередь увеличивает возможность получения стабильной доходности.

Итак, корреляция имеет важное значение в теории портфеля. Это показатель, который позволяет инвестору оценить связь между различными активами в портфеле

Инвестор может использовать корреляции для диверсификации и управления рисками, что помогает ему достичь максимальной доходности при заданном уровне риска.

Корреляционный анализ

Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).

Ограничения корреляционного анализа

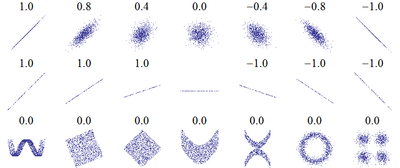
Множество корреляционных полей. Распределения значений (x,y){\displaystyle (x,y)} с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.

Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.
Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.
Исходная совокупность значений должна быть качественно однородной.
Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.

Область применения

Данный метод обработки статистических данных весьма популярен в экономике, астрофизике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.

Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

Коэффициент «бета»: как его использовать для определения чувствительности к риску рынка?

Одним из индикаторов, отражающих чувствительность набора финансовых инструментов к системному рыночному риску, является бета. Этот индикатор демонстрирует уязвимость портфеля к глобальным рыночным происшествиям, над которыми инвестор власти не имеет.

Коэффициент бета — это индикатор, характеризующий направление и степень изменения стоимости финансового инструмента по отношению к рынку. Под последним, как правило, понимается индекс S&P 500, покрывающий 80% рыночной капитализации США и служит индикатором экономики США.

Бета может быть рассчитана для конкретной акции, так и для инвестпортфеля в целом. Для определения этого показателя, поведение актива сравнивается с эталоном в течение определенного периода времени. Например, Мосбиржа дает информацию о ежедневных бета-оценках для российских эмитентов по результатам 30-ти торговых сессий.

Давайте разберемся, о чем говорят те или иные значения:

0 <бета<1 — актив движется в одну сторону с S&P 500, но не колеблется так сильно — риск ниже рыночного.
−1 <бета<0 — корреляция между активом и эталоном обратная. Они движутся в разные стороны, но актив ведет себя более стабильно.
Бета <−1 — корреляция отрицательная, но актив несет больший риск, чем рынок.
Бета > 1 – корреляция положительная, но волатильность выше рынка.

Давайте рассмотрим на реальном примере. Допустим, в портфель инвестора включены четыре актива.

«Бета»	Доля
Актив А	1	25%
Актив B	1,6	25%
Актив C	0,75	25%
Актив D	0,5	25%

В этом случае общая «бета» портфеля рассчитывается следующим образом.

25% × 1 + 25% × 1,6 + 25% × 0,75 + 25% × 0,5 = 0,96

В результате, бета оказалась близкой к единице. Это означает, что риск портфеля сопоставим с риском S&P 500. Допустим, инвестор хочет получить более высокую доходность и готов пойти на больший риск: его устраивает бета-коэффициент портфеля, равный 1,2. Это может быть достигнуто путем корректировки долей активов. Например: мы берем по 5% актива A и по 10% активов C и D в пользу наиболее рискованного актива — B.

Итак, мы получаем новую бету кошелька:

20% x 1 + 50% x 1,6 + 15% x 0,75 + 15% x 0,5 = 1,19

Чтение коэффициентов корреляции

После ввода в Excel формулы, вы увидите цифры от -1 до 1. Чем ближе к 1, тем теснее связь между активами, т.е. графики движутся синхронно. Отрицательные значения показывают обратную связь, т.е. если один инструмент снижается в цене, другой – растёт. Тесной считается корреляция от 0.8 до 1 (или от -0.8 до -1). Распределение капитала между несколькими инвестиционными активами, которые коррелируют с коэффициентом больше 0.8, нельзя считать диверсификацией. Фактически, такое распределение не менее рискованно, чем вложение всех денег в один инвестиционный актив.

Для целей диверсификации следует выбирать активы, связь между которыми меньше 0.6. На практике найти их не так просто – чем шире диверсификация, тем сложнее найти инвестиционный инструмент, который не коррелирует со всеми остальными. Большая ошибка – сравнивать только 2 актива и на этом основании заносить их в портфель. Проще всего найти несвязанные друг с другом инструменты на фондовом рынке, особенно если инвестор не ограничивает себя одной биржей.

Определение и основные принципы

Корреляция — это статистическая мера, используемая для определения взаимосвязи или взаимозависимости между двумя или более переменными. В контексте инвестирования, корреляция оценивает степень, в которой изменения одной инвестиции связаны с изменениями другой инвестиции.

Основные принципы корреляции в инвестировании включают:

Корреляционный коэффициент — это числовой показатель, который позволяет оценить силу и направление взаимосвязи между двумя переменными. Корреляционный коэффициент может принимать значения от -1 до 1. Значение 1 означает положительную корреляцию, значение -1 — отрицательную корреляцию, а значение 0 — отсутствие корреляции.
Инвестиционный портфель — это комбинация различных инвестиций, которые управляются инвестором. Портфель может состоять из акций, облигаций, фондов и других активов. Корреляция между инвестициями в портфеле может помочь инвестору снизить риск и достичь более стабильной доходности.
Диверсификация — это стратегия инвестирования, которая заключается в распределении инвестиций между различными активами для снижения риска. При диверсификации портфеля инвестор стремится создать комбинацию инвестиций, которые имеют низкую или нулевую корреляцию между собой. Это позволяет снизить общий риск портфеля.
Позитивная и негативная корреляция — показывают направление взаимосвязи между переменными. Позитивная корреляция означает, что две переменные движутся в одном направлении: если одна переменная растет, то и другая увеличивается. Негативная корреляция означает, что две переменные движутся в разных направлениях: если одна переменная растет, то другая уменьшается.
Корреляционная матрица — это таблица, которая представляет собой совокупность корреляционных коэффициентов между различными парами переменных. Корреляционная матрица помогает инвесторам анализировать взаимосвязь между различными инвестициями и принимать информированные решения о создании или изменении инвестиционного портфеля.

Определение и понимание корреляции в инвестировании помогает инвесторам принимать обоснованные инвестиционные решения, строить эффективные портфели и управлять рисками. Корреляционный анализ является важным инструментом в инвестиционной стратегии и помогает инвесторам достичь своих финансовых целей.

Значение слова «корреляция»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Математической мерой корреляции двух случайных величин служит корреляционное отношение

либо коэффициент корреляции

). В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.

Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.

КОРРЕЛЯ’ЦИЯ, и, ж. (науч.). 1. Соотношение, взаимная зависимость сопоставляемых понятий (филос.). 2. Взаимная связь явлений, находящихся в известной зависимости друг от друга. Рост безработицы и количество уголовных преступлений находятся в прямой корреляции друг к другу.

корреля́ция

1. матем. статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми) ◆ Высок коэффициент парной корреляции между переменными x₁ и x₃ (коэффициент корреляции 0,9), что показывает их тесную корреляционную взаимосвязь. К. М. Семенович, Б. П. Чупрынов, «Математика для экономистов: Учебное пособие», 2015 г. (цитата из библиотеки Google Книги) ◆ Если, когда увеличивается одно значение, то в большинстве случаев увеличивается и второе, корреляция положительная, а если одно значение уменьшается при увеличении второго, то тут корреляция уже отрицательная, или обратная. Пример отрицательной корреляции — график, показывающий, как соотносится температура воздуха с высотой над уровнем моря. Чем выше на гору вы забираетесь, тем холоднее воздух. М. Эскью, Р. Истуэй, «Математика с удовольствием!», 2017 г. (цитата из библиотеки Google Книги)

2. психол. взаимное соотношение, соответствие понятий и явлений ◆ Всё большее количество фактов поддерживают теорию, согласно которой существует корреляция между Я-концепцией и успеваемостью в школе. У успешных учеников более развитое чувство достоинства, и они в какой-то мере лучше относятся к себе (Garzarelli, Ever art, and Lester, 1993). Тем не менее эта связь обратима. Те, у кого высокая самооценка, лучше учатся в школе, а те, кто хорошо учится в школе, имеют более высокую самооценку… Ф. Райс, «Психология подросткового и юношеского возраста», 2010 г. (цитата из библиотеки Google Книги) ◆ Положительные, но умеренные по величине корреляции между учебными оценками и результатами тестирования не позволяли исследователям однозначно утверждать, что интеллект детерминирует успешность обучения. В. Н. Дружинин, «Психология общих способностей. 3-е изд.», 2013 г. (цитата из библиотеки Google Книги) ◆ «Корреляция» в прямом переводе означает соотношение. Если изменение одной переменной сопровождается изменением другой, то говорят о корреляции этих переменных. Наличие корреляции двух переменных не является свидетельством наличия причинно-следственных зависимостей между ними, но даёт возможность выдвинуть такую гипотезу. Отсутствие корреляции позволяет опровергнуть гипотезу о причинно-следственной связи переменных. М. Коновалова, «Экспериментальная психология: конспект лекций», 2017 г. (цитата из библиотеки Google Книги)

3. книжн. взаимная связь явлений, соотношение ◆ Корреляция между атмосферным давлением и влажностью воздуха. ◆ Количество уголовных преступлений и рост безработицы находятся друг к другу в прямой корреляции.

4. биол. взаимная согласованность функций частей и строения и животного или растения, которая поддерживает постоянство его внутренней среды и является следствием приспособления организма к условиям его существования ◆ Закон корреляции (Ж. Кювье, 1793): в организме, как целостной системе, все его части соответствуют друг другу как по строению, так и по выполняемым функциям. Р. Е. Михайловна, ‎Ш. Т. Матвеевна, ‎Ш. Л. Алексеевна, «Биология (Учебник)», 2016 г. (цитата из библиотеки Google Книги)

5. лог. отношение между двумя одинаковыми по форме связями; в случае, если одна связь становится изоморфной другой, тогда это — корреляция, а само закономерное структурное изменение – коррелятор

A/B-тестирование для проверки наличия причинно-следственной связи

Вы наблюдаете корреляцию между событиями X и Y. Но для принятия решения вам нужно понять, есть ли между ними причинно-следственная связь.

Для ответа на этот вопрос надо провести эксперимент.

Например, когда одна группа пользователей получает фичу, а другая нет. Все остальные условия для них идентичны. По итогам теста собираются и анализируются данные. На их основе вы можете понять, оказала ли фича влияние на интересующую нас метрику.

Хотя порядок действий и звучит просто, на деле проведение A/B-тестов требует внимания ко множеству деталей и дисциплины. В частности, вам нужно быть очень аккуратными, чтобы не спутать случайное изменение в значение целевой метрики с влиянием тестируемого изменения. Для этого используется понятие статистической значимости — подробнее об этом читайте здесь.

Корреляция на форексе

Распространённая стратегия, основанная на корреляции валютных пар, заключается в том, что в случае резкого отклонения коэффициента корреляции от текущего значения, сделки открываются в направлении восстановления этого значения. Например, если пары EURUSD и GBPUSD длительное время двигались в одном направлении, то при их сильном расхождении можно ожидать сближения, если расхождение не вызвано долговременными фундаментальными факторами (например, изменение учётной ставки).

Кроме того, корреляция валютных пар используется при комплексной оценке рынка. Например, накануне ипотечного кризиса 2008—2009 годов, когда австралийский и новозеландский доллары, а также английский фунт имели высокую ключевую ставку, большое развитие получила стратегия торговли под названием carry trade. Она заключалась в том, что при благоприятных для фондовых рынков событиях особенно активно росли пары этих валют с иеной, традиционно отличающейся очень низкой ставкой, они же и активно снижались при неблагоприятных событиях.

При том, что никакая корреляция не может затрагивать абсолютно все временные интервалы и возможны разнонаправленные движения валют, но ярко выраженное однонаправленное движение, как правило, говорит о наличии общего фундаментального «драйвера». Это облегчает планирование сделок. В частности, нет смысла искать откаты и внутри дня работать против тренда, если все чётко коррелирующие пары идут в одном направлении.

Посмотреть таблицу корреляции валютных пар и некоторых других инструментов в реальном времени можно на myfxbook.com/forex-market/correlation. Из этой таблицы видно, что практически не коррелируют между собой пары EURUSD и AUDCAD. В случае одновременного открытия сделок по этим парам можно не опасаться ни суммирования убытков, ни перекрывания прибыли по одной паре убытком по другой.

На этом графике показано, как австралийский и новозеландский доллары, обратно коррелирующие с «валютами-убежищами» иеной и швейцарским франком, активно росли в период наибольшего дифференциала ключевых ставок. Эта тенденция сменилась на противоположную после того, как с углублением ипотечного кризиса начался период срезания ставок.